Just Intonation
Just intonations are tuning systems in which pitches follow physically relevant ratios. The mechanics of making instruments has, for a very long time, dictated the use of equal tempered instruments. Without equal temperment, retuning adjustments will need to be made when playing in different keys. Equal temperment that uses a small number of pitches also makes the mechanical instruments easier to build because there are less parts.
But with electronic music, the justifications for only sticking to the 12 tone system no longer hold. Now it is just an issue of what people are in the habit of playing and listening to. With the rise of touchscreens as controllers, fretless controllers that can do dynamic intonation will become more common. Pythagoras started out as an attempt to do dynamic intonation. But when I got things working, 53ET became a defacto feature of it that emerged on its own. I eventually gave up on actual harmonics based intonation and just went with 53ET because it was so close, within the exact pixel in almost all cases, to the real spectrum locations.
I don't aim to expand upon this too much into the realm of academic microtonality. This is something that is designed to be practical. So instead of learning by generating big lists of floating point numbers and ratios for you to ponder and bamboozling you with equations, I am building geometry into an instrument that allows these ideas to be used and tested in practice. There is a little bit of multiplication going on, because that's easier than giving every little ratio a weird name for you to remember.
There is only so much you can do with timbre to make an instrument sound interesting. Getting the correct intonation is the first thing that almost all MIDI based instruments are giving up on. The pitches need to go in correct, and cannot be corrected by cleverness in the engine. Two waves in perfect ratios form a standing wave of a new shape, and do not come out as two separate notes. The octave is the only interval that we are used to hearing completely correctly, and the fifths and fourths are reasonably close. All the other intervals could use improvement by exploring the spectrum outside the normal 12 notes.
Relating Actual Harmonic Geometry to 53ET
I have posted before about the 53 note
 per octave scale, 53ET, with some lower quality images of its pattern. It is a highly special tuning system that captures the behavior of the spectrum in a practical way. It is explicitly used in Turkish Makam, a classical music system. A subset of this scale shows up in some form just about everywhere that flexible tuning instruments such as violin, sitar, and voice are used. The 12 tone system that we are all familiar with is interesting in its own way, but there is very little about that system that readily connects with the reality of the spectrum in an obvious way. The more you dig into 53ET, the more you feel like you have stumbled upon some ancient Magick. It really is a special system, and is much deeper than the 12 tone system we are used to.
per octave scale, 53ET, with some lower quality images of its pattern. It is a highly special tuning system that captures the behavior of the spectrum in a practical way. It is explicitly used in Turkish Makam, a classical music system. A subset of this scale shows up in some form just about everywhere that flexible tuning instruments such as violin, sitar, and voice are used. The 12 tone system that we are all familiar with is interesting in its own way, but there is very little about that system that readily connects with the reality of the spectrum in an obvious way. The more you dig into 53ET, the more you feel like you have stumbled upon some ancient Magick. It really is a special system, and is much deeper than the 12 tone system we are used to.
Starting with a clean slate. Forget all about the twelve tone scale. Just think about a reference tone at some middle frequency, like a drone note. It doesn't matter what it's actual frequency is, because microtonality is about well defined relationships in a relative sense.In the top figure, we have a note that's a reference note of 1. It is in some rows that are stacked by pure fourths. Every note emits overtones that can lock with notes up above it. So the lines going up out of a note are the overtones that it emits. The lines going down are notes that can have an overtone that goes into our note. The unmarked line at an angle of about 2 o'clock is actually marked 2, the octave overtone.
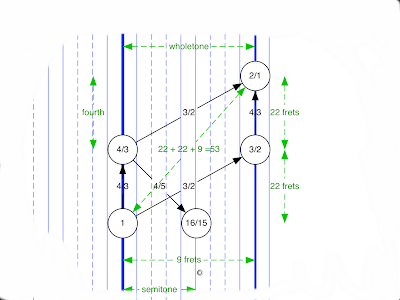
The pitch ratios are simple numbers in accordance with the harmonic series, (N+1)/N. That is to say, 2/1, 3/2, 4/3, 5/4, 6/5, ... 16/15, ... 81/80,... etc. In this system moving up to a string multiplies the pitch times 4/3, because we are tuned to the pitch ratio of a Just fourth - which is 4/3. It happens to be 22 frets of 53ET along the same string. So we treat going exactly up to be the same as going 22 frets to the right. (It's the same concept as a bass guitar, where going up 5 frets is the same as jumping up to the next string.) So this second diagram shows whole tones as the most important unit, which is roughly two chromatic notes. ie: A to B for example. I managed to forget to note the fact in the drawings anywhere, but that whole tone is the ratio 9/8 ((N+1)/N, so that means that it's a special part of the harmonic series).
So any notes that are in the scale have some short path along these lines where you pick a note and draw out harmonics from it as the first diagram does. So, if we start at pitch 1, take the route 4/3 by going straight up, then the path 3/2 by taking that diagonal, these numbers multiply to give us the number 2. That is the definition of octave; twice the original frequency. 4/3 is called a "fourth", and 3/2 is called a "fifth", 2 is "octave", 1 is "root". And note that we can get a semitone of sorts by following 4/3 up, but travel down to 4/5 to land on 16/15. This means that if you chord the notes 16/15 and 1 together, 16/15 has major third overtone at 4/3, and the 1 has a fourth overtone at 4/3, so they are consonant because they link up by a short path. Notice also that even though we reached 16/15 by navigating that it's (N+1)/N, which means that it shows up on the harmonic series if we go far enough, as does 9/8.
And I do in fact mean to chord two notes so close to each other, an "A" and a Just semitone of "Bflat" 16/15 will sound like trash on a piano. It's a reasonable chord in this system because it's 1 versus 16/15 rather than 1 versus 2^(1/12), which isn't very close to any reasonable integer ratio.
So this whole system ignores the really high harmonic ratios and uses the ones that you can create from nothing more than octave, fourth, major third relationships. It happens to be that octave (2) and undertone (1/2) are related, as are fourths (4/3) and fifths (3/2), and the major and minor thirds. What is more is that if you pick out all the prime numbers in their ratios, then this system is everything you can make only out of the numbers involving 2, 3, 5; the first three prime numbers. This gives a way to "measure" how closely related two pitches are. There are no note names here, just relative relationships by pitch.
The real enlightening moment for me was when I had fixed a bug in the drawing that had caused major and minor third to not hit exact 53ET frets, that everything locked together very tightly. I could hear this and knew this long before I had the drawing right; I let my wrong math overrule what was obvious to my ears. So, here is an explaination of *why* major and minor triads are special.

When you play a minor third interval, there are 9 steps to the first wholetone (9/8) which are reached by 3/2 * 3/4 = 9/8. But from the fifth (3/2), you can take a major third down by 4/5 to reach 1 * 3/2 * 4/5 = 6/5. So the ratio 6/5 is the minor third as noted in the harmonic series above. 6/5 has a minor third harmonic coming off of it, and the root has a fifth coming off of it and they meet at the same point.
Similarly if you play the root and major third together, you can see that there is a minor third harmonic coming off of it that meets at the same fifth that the root meets. These two chords are simply stacks of a major and minor third, but in a different order. These three notes together along with the octave relate: 1/1, 2/1, 3/2, 4/3, 5/4, 6/5 all simultaneously. They form a rich set of harmonics in that sense. That's why triads are special.

One thing to keep in mind about 53ET though is that it's very close to a complete system that captures all octave, fifth, major third relationships. It is not exact in a mathematical sense. But it is very close, much closer than the 12 tone system, in the sense that you will only be able to discern larger ratios to a reasonable degree of accuracy and it's a very practical approximation to the spectrum.
Note: The scale I am showing up above is not using the Pythagorean choice for the third and the sixth. A semitone is generally going to be 4 frets rather than 5 when in those cases. Pythagorean scales are generally a span of notes that are adjacent in the Just circle of fifths (or fourths... same result), which causes third and sixth to come out one fret flatter if done that way. So my scale is considered wrong if the goal is Pythagorean tuning, or might be acceptable if you favor being closer to Just major thirds and Just minor thirds. Transposition is easier if the Pythagorean choice is taken. There is a short harmonic path between both choices, so it's really a matter of what it is you are trying to do. (I am getting authoritative information from somebody that actually does Makam, and I am trying to make sure that I am doing things right. :-) )
Another interesting thing about 53ET is that it contains the interval that is the difference between a pure major third (5/4) and two whole tones (9/8 * 9/8 = 81/64). This difference creates a lot of controversy in tuning systems. There is a tension between wanting something that is simple and tunable by ear using only fifths and octaves, and the close to major third tone that a simple Pythagorean tuning gives. So, 81/80 shows up in a lot of places related to tuning, in Indian music, etc. This interval causes a situation where the scale may not want to follow the simplest ratios created by following the fourths and fifths. In a minor-like scale, there will be a tendency to make minor third, minor sixth and the seventh one fret sharper than you might guess if you did the geometry without listening to the result.
A Note On Accuracy
If you go through this and verify the intervals (as my Makam playing friend did), you will find that you have to be careful about how you interpret the geometric picture. If we assume that going up is multiplying by exactly 4/3, then the path that you compute to an interval will be exact. It's a simple matter of multiplying ratios.
But that doesn't mean that it lands exactly on a a 53ET fret. But you can tell from actually playing Geo Synth that it is close to a high level of accuracy, and see exactly how far off it is when it's not exactly to the pixel on the screen. When doing all navigation as pure 3-limit, you will always get exact numbers (ie: 2, 1/2, 3/4, 4/3 are the navigational options, all else is derived) if you don't treat the circle of Just Fifths as closed, and make sure that you only navigate a span of 53 fifths without trying to wrap around at the point where it almost closes. However, it still applies that the 53ET frets themselves are an approximation, as 2^(1/53) is an irrational number.
It gets even more complicated when we declare that the interval 00 05 is a minor third and 00 08 is a major third (see tablature below). You can have different paths that reach the same fret, but don't come out to the exact same ratio. But this is ok, because if you subtract one ratio from the other you get a very small number that can be considered zero for all practical purposes; especially because we pick *shortest* path to determine how a ratio is created.
This problem was proposed to me:
I am at A. Where is F?
... navigate down two whole tones
8/9 * 8/9
= 2^6 * 3^-4
... navigate up four fourths then two octaves back down to get into range
(4/3)^4 * 2^-2
= 4^4 * 3^-4 * 2^-2
= 2^8 * 3^-4 * 2^-2
= 2^6 * 3^-4
These are the same because they use 3-limit intervals. But when we use paths involving the 5-limit, they don't come out identical. I was given 405/512. So I try to factor it into a path:
405/512 =
810/1024 =
81 * 10 / 1024 =
81 * 5 / 512 =
2^-9 * 3^4 * 5 =
5/4 * 2^-7 * 3^4 =
(3/2)^4 * 5/4 * 2^-3 =
(9/4)^2 * 5/4 * 2^-3 =
(9/8)^2 * 5/4 * 2^-1
up two wholetones, up a maj third, down an octave. But subtracting these intervals:
64/81 - 405/512 = -0.0000892168...

They are practically the same value, so both landed at the same fret. So, if you mix in 5-limit , then don't use high powers of them and accuracy will not get out of control. The use of this is that you can do the geometry in your head, and if you do it carefully it will be exact. But you can use approximations without the number crunching via 53ET.
Tablature

When I was faced with writing tablature for 53ET, I thought that the idea of notating with large fret numbers was ridiculous. Instead I took a different approach, that is compatible with 12ET tablature once you get used to it.
The dark blue lines every 9 lines in my grid are the markers for whole tones (9/8). In 53ET, whole tones cannot be split into exact semitones because they are split into 9 subdivisions. So the first numerical digit notes which dark blue line (marking a whole tone boundary), while the second digit denotes the lighter line above the whole tone division.
One interesting property that this has is that if you pretend that these are actually decimal numbers with a decimal in between them and multiply them times 2 (ie: "15" x 2 = 30 ... think of as 3.0); the numbers round off into the same locations as their 12ET tablature counterparts.
Ex: 00 06 15 becomes... 0.0 1.2 3.0 ... or 0 1 3 in guitar tab, where it's obvious that the middle note is intended to be sharper. But the notation is completely unambiguous. It tells you exactly what frets to put your fingers on, without making up strange symbols to try to add to the standard music system. (Note: I am targeting guitarists. Almost no guitarists fluently read standard music notation, and it's not really necessary for this.)
Geo Synth (Pythagoras)
So the main idea that got Pythagoras started (now called Geo Synth) was geometry. I wanted to avoid any equal tempered system, or anything artificial that didn't come from the spectrum itself. But when I draw out the 3-limit, which is the closure of all fourths and fifths (up to some reasonable distance) then it became 53ET. It was never my plan to support 53ET. It came to me. And it wasn't until recently that I realized that my ears were right and my drawings for the thirds were wrong, and fixed the drawings. Now the major and minor lines draw straight through 53ET frets. It is now clear that even the ratios 7/6 and 8/7 which are up next are not too far from 53ET as long as you only navigate that ratio once.

Here is a quick video picking out some of the obvious intervals:
http://www.youtube.com/watch?v=eViP4cJYvvE
The idea behind the interface was as explained above, to show all of the harmonics coming off of a note. You line them up until they lock visually. When they lock visually, the sound is obviously consonant.
So I have the normal twelve pitch system drawn over it, as well as quartertones (ie: 24Et which includes the normal 12 tones).
24ET is roughly the official Arabic intonation system. It doesn't line up so well with the harmonic series. It's main point is to take a core pentatonic scale, and don't play semitone stretches. Whenever you encounter a minor third, the note in the dead center between them (median second) is what you want to play. These are what I would call "red notes" on a piano. If you had red keys where black keys are missing between E/F and B/C on piano, they would have to be quartertone "red notes".
I think touch screens will usher in some initial experimentation with these kinds of scales at first. But after a while, it will sink in that Phrygian scales and Harmonic Minor scales are bad imitations of the Arabic system (especially Phrygian sharp fourth), and people will start adopting actual Maqam scales for certain scenarios. Then people will realize that with 53ET you can do this, while also getting even better chords out of it than we are accustomed to getting.

